Упражнение 489 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 144

а) \(\begin{cases} x^2 - y + 11 = 0,\\ y + x^2 = 4 \end{cases}\)

\(\begin{cases} y = x^2 + 11,\\ y =- x^2 + 4 \end{cases}\)

\(y = x^2 + 11\) - парабола, полученная из параболы \(y = x^2\), с вершиной в точке \((0; 11)\), ветви вверх.

\(y = - x^2 + 4\) - парабола, полученная из параболы \(y = -x^2\), с вершиной в точке \((0; 4)\), ветви вниз.

Ответ: решений нет.

б) \(\begin{cases} (x + 3)^2 + (y + 4)^2 = 1,\\ (x - 2)^2 + (y - 1)^2 = 4 \end{cases}\)

\((x + 3)^2 + (y + 4)^2 = 1\) - окружность с центром в точке \((-3; -4)\) и радиусом \(r = 1\).

\((x - 2)^2 + (y - 1)^2 = 4\) - окружность с центром в точке \((2; 1)\) и радиусом \(r = 2\).

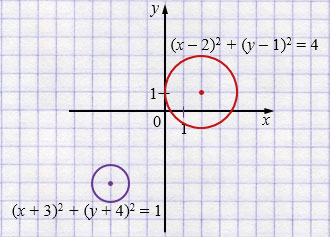
Ответ: решений нет

в) \(\begin{cases} y = |x|,\\ \dfrac{1}{2}x^3 - y = 0 \end{cases}\)

\(\begin{cases} y = |x|,\\ y = \dfrac{1}{2}x^3 \end{cases}\)

\(y = |x|\),   \(y \ge 0\).

\(y = \dfrac{1}{2}x^3\) - кубическая парабола, I и III координатные четверти.

Пояснения:

Для решения систем уравнений графическим способом строят графики каждого уравнения и находят точки их пересечения. Количество точек пересечения графиков уравнений соответствует количеству решений системы.