Упражнение 488 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 144
Вернуться к содержанию учебника
Вопрос
Решите графически систему уравнений:
а) \(\begin{cases} y+x+x^2=0, \\ x-y=10; \end{cases}\)
б) \(\begin{cases} (x-2)^2+y^2=9, \\ y=x^2-4x+4; \end{cases}\)
в) \(\begin{cases} x^2+y^2=25, \\ y=2x^2-14; \end{cases}\)
г) \(\begin{cases} x^2+y^2=10, \\ xy=3; \end{cases}\)
д) \(\begin{cases} x+y=8, \\ (x+1)^2+y^2=81; \end{cases}\)
е) \(\begin{cases} y=-x^2+4, \\ y=|x|. \end{cases}\)
Подсказка
Вспомните:
- Системы уравнений с двумя переменными.
- Уравнения с двумя переменными.
- Координаты точки на координатной плоскости.
- Квадратичная функция, ее график.
- Уравнение окружности, ее график.
- Линейная функция, ее график.
- Функция обратной пропорциональности, ее график.
- Модуль числа.
Ответ
а) \(\begin{cases} y+x+x^2=0, \\ x-y=10 \end{cases}\)
\(\begin{cases} y=-x-x^2, \\ y=x-10 \end{cases}\)
1) \(y = -x^2 - x\)
\(y = -(x^2 + x)\)
\(y = -((x^2 + x + 0,5^2) - 0,5^2)\)
\(y = -((x + 0,5)^2 - 0,25)\)
\(y = - (x+ 0,5)^2 + 0,25\) - парабола, полученная из параболы \(y = -x^2\) с вершиной в точке \((-0,5; 0,25)\), ветви вниз.
2) \(y=x-10\) - прямая.
| \(x\) | \(0\) | \(5\) |
| \(y\) | \(-10\) | \(-5\) |

Ответ: \((-4,3; -14,3),\;(2,3; 7,7)\).
б) \(\begin{cases} (x-2)^2+y^2=9, \\ y=x^2-4x+4 \end{cases}\)
1)\((x-2)^2+y^2=9\) - окружность с центром в точек \((2; 0)\) и радиусом \(r = 3\).
2) \(y=x^2-4x+4\)
\(y =(x - 2)^2\) - парабола, полученная из параболы \(y = x^2\), с вершиной в точке \((2; 0)\), ветви вверх.
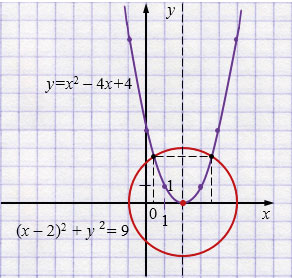
Ответ: \((0,4; 2,5)\), \((3,6; 2,5)\).
в) \(\begin{cases} x^2+y^2=25, \\ y=2x^2-14; \end{cases}\)
1) \(x^2+y^2=25\) - окружность с центром \((0; 0)\) и радиусом \(r = 5\).
2) \(y=2x^2-14\) - парабола, полученная из параболы \(y = 2x^2\), с вершиной в точке \((0; -14)\), ветви вверх.

Ответ: \((-3;4)\), \((3; 4)\),
\((-2,2; - 4,5)\), \((2,2; -4,5)\).
г) \(\begin{cases} x^2+y^2=10, \\ xy=3; \end{cases}\)
\(\begin{cases} x^2+y^2=10, \\ y=\frac3x; \end{cases}\)
1) \(x^2+y^2=10\) - окружность с центром в точке с центром в точке \((0; 0)\) и радиусом \(r = \sqrt{10} \approx3,2\).
2) \(y = \frac3x\) - гипербола, ветви в I и III четвертях.
| \(x\) | \(0,5\) | \(1\) | \(3\) | \(6\) |
| \(y\) | \(6\) | \(3\) | \(1\) | \(0,5\) |
| \(x\) | \(-6\) | \(-3\) | \(-1\) | \(-0,5\) |
| \(y\) | \(-0,5\) | \(-1\) | \(-3\) | \(-6\) |

Ответ: \((1;3),\;(3;1),\;(-1;-3),\;(-3;-1)\).
д) \(\begin{cases} x+y=8, \\ (x+1)^2+y^2=81 \end{cases}\)
\(\begin{cases} y=8-x, \\ (x+1)^2+y^2=81 \end{cases}\)
1) \(y = 8 - x\) - прямая.
| \(x\) | \(0\) | \(8\) |
| \(y\) | \(8\) | \(0\) |
2) \((x+1)^2+y^2=81\) - окружность с центром \((-1; 0)\) и радиусом \(r = 9\).

Ответ: \((8;0),\;(-1;9)\).
е) \(\begin{cases} y=-x^2+4, \\ y=|x| \end{cases}\)
1) \(y =-x^2+4\) - парабола, полученная из параболы \(y=-x^2\) с вершиной \((0; 4)\), ветви вниз.
2) \(y=|x|\)
| \(x\) | \(-3\) | \(0\) | \(3\) |
| \(y\) | \(3\) | \(0\) | \(3\) |

Ответ: \((-1,6; 1,6)\), \((-1,6; 1,6)\).
Пояснения:
Решения системы — это точки пересечения графиков двух уравнений.
Вернуться к содержанию учебника