Упражнение 374 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 116

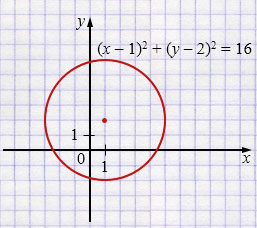
а) \((x - 1)^2 + (y - 2)^2 = 16\)

\((x - 1)^2 + (y - 2)^2 = 4^2\)

Центр окружности \((1;\,2)\), \(r = 4\)

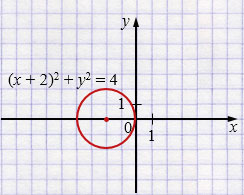
б) \((x + 2)^2 + y^2 = 4\)

\((x + 2)^2 + y^2 = 2^2\)

Центр окружности \((-2;\,0)\), \(r = 2\)

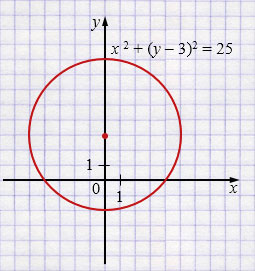
в) \(x^2 + (y - 3)^2 = 25\)

\(x^2 + (y - 3)^2 = 5^2\)

Центр окружности \((0;\,3)\), \(r = 5\)

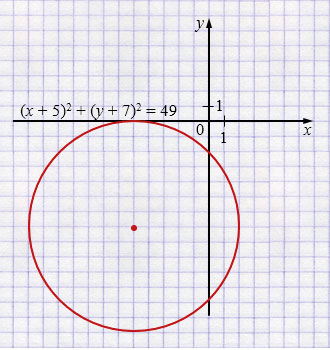
г) \((x + 5)^2 + (y + 7)^2 = 49\)

\((x + 5)^2 + (y + 7)^2 = 7^2\)

 Центр окружности \((-5;\,-7)\), \(r = 7\)

Пояснения:

Основная формула:

\[ (x - a)^2 + (y - b)^2 = r^2, \]

где \((a; b)\) — центр окружности, а \(r\) — её радиус.

Определив по уравнению центр и радиус окружности, строим ее с помощью циркуля.