Упражнение 385 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 121
Вернуться к содержанию учебника
Вопрос
Решите систему уравнений графически и аналитически:
а) \(\begin{cases} x^2 + y^2 = 16,\\ x - y = 4; \end{cases}\)
б) \(\begin{cases} y = x^2 + 1,\\ x + 2y = 5. \end{cases}\)
Подсказка
Вспомните:
- Что называют решением системы уравнений с двумя переменными, графический способ решения систем уравнений с двумя переменными.
- Координаты точки на координатной плоскости.
- Метод подстановки при решении систем уравнений.
- Уравнения с двумя переменными, их свойства.
- Линейная функция, ее график.
- Уравнение окружности, ее график.
- Квадратичная функция, ее график.
- Полные квадратные уравнения.
- Неполные квадратные уравнения.
- Арифметический квадратный корень.
- Распределительное свойство умножения.
- Квадрат суммы двух выражений.
- Подобные слагаемые.
- Степень с натуральным показателем.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Деление и дроби.
- Десятичная запись дробных чисел.
- Умножение десятичных дробей.
- Сложение и вычитание десятичных дробей.
Ответ
а) Графический способ:
\(\begin{cases} x^2 + y^2 = 16,\\ x - y = 4 \end{cases}\)
\(\begin{cases} x^2 + y^2 = 16,\\ y = x - 4 \end{cases}\)
\( x^2 + y^2 = 16\) - окружность с центром в точке \((0; 0)\) и \(r = 4\).
\(y = x - 4\) - прямая.
| \(x\) | \(0\) | \(4\) |
| \(y\) | \(-4\) | \(0\) |
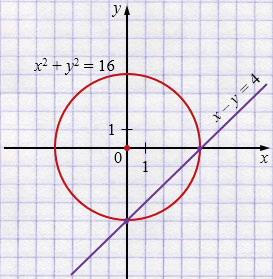
\((0; -4)\), \((4; 0)\) - решения системы.
Аналитический способ:
\(\begin{cases} x^2 + y^2 = 16,\\ x - y = 4 \end{cases}\)
\(\begin{cases} x^2 + y^2 = 16,\\ x = y + 4 \end{cases}\)
\((y+4)^2 + y^2 = 16\)
\(y^2 + 8y + 16 + y^2 - 16 = 0\)
\(2y^2 + 8y = 0\)
\(2y(y + 4) = 0\)
\(y = 0\) или \(y + 4 = 0\)
\(y = -4\)
Если \(y = 0\), то
\(x = 0 + 4= 4\).
Если \(y = -4\), то
\(x = -4 + 4 = 0\).
Ответ: \((4; 0)\), \((0; -4)\).
б) Графический способ:
\(\begin{cases} y = x^2 + 1,\\ x + 2y = 5 \end{cases}\)
\(\begin{cases} y = x^2 + 1,\\ 2y = -x + 5 / : 2 \end{cases}\)
\(\begin{cases} y = x^2 + 1,\\ y = -0,5x + 2,5 \end{cases}\)
\(y = x^2 + 1\) - парабола, ветви которой направлены вверх.
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(10\) | \(5\) | \(2\) | \(1\) | \(2\) | \(5\) | \(10\) |
\(y = -0,5x + 2,5\) - прямая.
| \(x\) | \(1\) | \(3\) |
| \(y\) | \(2\) | \(1\) |

\((1; 2)\), \((-1,5; 3,25)\) - решения системы.
Аналитический способ:
\(\begin{cases} y = x^2 + 1,\\ x + 2y = 5 \end{cases}\)
\(\begin{cases} y = x^2 + 1,\\ x + 2(x^2 + 1) = 5 \end{cases}\)
\(x + 2(x^2 + 1) = 5\)
\(x + 2x^2 + 2 - 5 = 0\)
\(2x^2 + x - 3 = 0\)
\(D = 1^2 - 4\cdot2\cdot(-3) =\)
\(= 1 + 24 = 25 > 0\) - 2 корня.
\(\sqrt{25} = 5\).
\(x_1 = \dfrac{-1 + 5}{2\cdot2}=\dfrac{4}{4}=1\).
\(x_2 = \dfrac{-1 - 5}{2\cdot2}=\dfrac{-6}{4}=-\dfrac{-3}{2} =\)
\(=-1,5\).
1) Если \(x = 1\), то
\(y = 1^2 + 1= 2\).
2) Если \(x = -1,5\), то
\(y = (-1,5)^2 + 1 = 2,25 + 1 = 3,25\)
Ответ: \((1; 2)\), \((-1,5; 3,25)\) .
Пояснения:
Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение в верное равенство. Решить систему уравнений - это значит найти все ее решения или убедиться, что их нет.
Суть графического метода решения системы уравнений с двумя переменными:
1) построить на одной координатной плоскости графики уравнений, входящих в систему;
2) найти координаты всех точек пересечения построенных графиков;
3) полученные пары чисел и будут искомыми решениями.
Чтобы решить систему аналитически, использовали метод подстановки:
1) выразить из любого уравнения системы одну переменную через другую;
2) подставить в другое уравнение системы вместо этой переменной выражение, полученное на первом шаге;
3) решить уравнение с одной переменной, полученное на втором шаге;
4) подставить найденное значение переменной в выражение, полученное на первом шаге;
5) вычислить значение другой переменной.
Квадратные уравнения вида
\( ax^2 + bx + c = 0\)
решаем через дискриминант:
\(D = b^2 - 4ac\).
Если \(D > 0\), то уравнение имеет 2 корня:
\( x = \frac{-b \pm \sqrt{D}}{2a}. \)
Вернуться к содержанию учебника