Упражнение 475 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 143

а) \(\begin{cases}x^2+3xy-10y^2=0,  / : y^2, \, y \ne0\\ x^2-4xy+3y=0\end{cases}\)

\(\begin{cases}(\frac xy)^2+3\frac xy-10=0, \\ x^2-4xy+3y=0\end{cases}\)

\((\frac xy)^2+3\frac xy-10=0\)

Пусть \(\frac xy = t\), тогда

\(t^2 + 3t - 10 = 0\)

\(D = 3^2 - 4 \cdot 1 \cdot (-10) = \)

\(=9 + 40 = 49 > 0\) - два корня.

\(\sqrt{49} = 7\).

\(t_1 = \frac{-3 + 7}{2\cdot1} = \frac42 = 2\).

\(t_2 = \frac{-3 - 7}{2\cdot1} = \frac{-10}{2} = -5\).

Если \(t = 2\), то

\(\frac xy = 2, \Rightarrow x = 2y\).

Если \(t = 2\), то

\(\frac xy = -5, \Rightarrow x = -5y\).

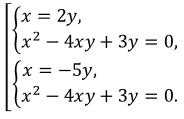
1) \(\begin{cases} x = 2y, \\ x^2-4xy+3y=0\end{cases}\)

\(\begin{cases} x = 2y, \\ (2y)^2-4\cdot2y\cdot y+3y=0\end{cases}\)

\( (2y)^2-4\cdot2y\cdot y+3y=0 \)

\( 4y^2-8y^2+3y=0 \)

\(-4y^2+3y=0 \)

\(y(-4y+3)=0 \)

\( y=0 \)  или   \(-4y + 3 = 0\)

                     \(-4y = - 3\)

                     \(y=\frac{3}{4} \)

                     \(y = 0,75\)

Если \(y=0\), то

\(x=2\cdot0=0\).

Если \(y=0,75\), то

\(x=2\cdot0,75= 1,5\).

2) \(\begin{cases} x = -5y, \\ x^2-4xy+3y=0\end{cases}\)

\(\begin{cases} x = -5y, \\ (-5y)^2-4\cdot(-5y)\cdot y+3y=0\end{cases}\)

\( (-5y)^2-4\cdot(-5y)\cdot y+3y=0 \)

\( 25y^2+20y^2+3y=0 \)

\(45y^2+3y=0 \)

\(3y(15y+1)=0 \)

\( y=0\)  или  \(15y + 1 = 0\)

                    \(15y = -1\)

                     \(y=-\frac{1}{15} \)

Если \(y=0\), то

\(x= -5\cdot0 = 0\).

Если \(y=-\dfrac{1}{15}\), то

\(x=-5\cdot\left(-\dfrac{1}{15}\right)=\dfrac{1}{3}\).

Ответ: \((0;0),\;(1,5;0,75),\)

\(\left(\dfrac{1}{3};-\dfrac{1}{15}\right).\)

б) \(\begin{cases}x^2+xy-6y^2=0, / : y^2, \, y \ne0\\ x^2+3xy+2y-6=0\end{cases}\)

\(\begin{cases}(\frac xy)^2+\frac xy-6=0,\\ x^2+3xy+2y-6=0\end{cases}\)

\((\frac xy)^2+\frac xy-6=0\)

Пусть \(\frac xy = t\), тогда

\(t^2 + t - 6 = 0\)

\(D = 1^2 - 4\cdot1\cdot(-6) =\)

\(=1 + 24 = 25 > 0\) - два корня.

\(\sqrt{25} = 5\).

\(t_1 = \frac{-1 + 5}{2\cdot1} = \frac42 = 2\).

\(t_2 = \frac{-1 - 5}{2\cdot1} = \frac{-6}{2} = -3\).

Если \(t = 2\), то

\(\frac xy = 2, \Rightarrow x = 2y\).

Если \(t = -3\), то

\(\frac xy = -3, \Rightarrow x = -3y\).

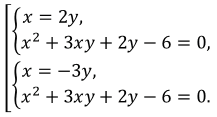
1) \(\begin{cases} x = 2y,\\ x^2+3xy+2y-6=0\end{cases}\)

\(\begin{cases} x = 2y,\\ (2y)^2+3\cdot2y\cdot y+2y-6=0\end{cases}\)

\( (2y)^2+3\cdot2y\cdot y+2y-6=0 \)

\( 4y^2+6y^2+2y-6=0 \)

\(10y^2+2y-6=0 \)  \(/ : 2\)

\(5y^2+y-3=0 \)

\( D=1-4\cdot 5\cdot(-3)=\)

\(=1+60=61 > 0\) - два корня.

\( y_{1,2}=\frac{-1\pm \sqrt{61}}{10} \)

Если \( y=\frac{-1 + \sqrt{61}}{10} \), то

\( x=\cancel2\cdot\frac{-1 + \sqrt{61}}{\cancel{10}_{\color{blue}{5}} }=\frac{-1 + \sqrt{61}}{5} \).

Если \( y=\frac{-1 - \sqrt{61}}{10} \), то

\( x=\cancel2\cdot\frac{-1 - \sqrt{61}}{\cancel{10}_{\color{blue}{5}} }=\frac{-1 - \sqrt{61}}{5} \).

2) \(\begin{cases} x = -3y,\\ x^2+3xy+2y-6=0\end{cases}\)

\(\begin{cases} x = -3y,\\ (-3y)^2+3\cdot(-3y)\cdot y+2y-6=0\end{cases}\)

\((-3y)^2+3\cdot(-3y)\cdot y+2y-6=0 \)

\(\cancel{9y^2}-\cancel{9y^2}+2y-6=0 \)

\(2y-6=0 \)

\(2y = 6\)

\(y = \frac62\)

\(y=3 \)

\(x=-3\cdot 3=-9\).

Ответ: \(\left(\dfrac{-1+\sqrt{61}}{5};\dfrac{-1+\sqrt{61}}{10}\right),\)

\(\left(\dfrac{-1-\sqrt{61}}{5};\dfrac{-1-\sqrt{61}}{10}\right),\,(-9;3),\).

Пояснения:

В каждой системе левая часть первого уравнения системы - однородный многочлен, то есть многочлен, каждый член которого имеет одну и ту же степень. Обе части эт ого уравнения разделили на \(y^2\), учитывая то, что \(y\ne0\). Получили квадратное уравнение относительно \(\frac xy\). При этом мы потеряем решение \((0; 0)\) первого уравнения системы. Но так как пара \((0; 0)\) не является решением второго уравнения, то система

а) \(\begin{cases}(\frac xy)^2+3\frac xy-10=0, \\ x^2-4xy+3y=0;\end{cases}\)

б) \(\begin{cases}(\frac xy)^2+\frac xy-6=0,\\ x^2+3xy+2y-6=0\end{cases}\)

является равносильной исходной системе.

Обозначив \(\frac xy\) буквой \(t\), в каждом случае получаем квадратное уравнение вида \(at^2 + bt + c = 0\), которое решаем через дискриминант \(D = b^2 - 4ac\). Если \(D > 0\),  то уравнение имеет два корня:

\(t_{1,2} = \frac{-b \pm \sqrt D}{2a}\).

Решив полученные квадратные уравнения, возвращаемся к замене \(\frac xy\) и выражаем переменную \(x\) через переменную \(y\), получаем совокупность систем уравнений, каждую систему решаем способом подстановки.