Упражнение 524 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 148

а) \(y(x^2+y^2-1)\ge 0\)

1) Если \(y\ge 0\), то

\(x^2+y^2-1\ge 0\)

\(x^2+y^2\ge 1\)

\(x^2+y^2 = 1\) - окружность с центром \((0; 0)\) и радиусом \(1\).

\(y = 0\) - ось \(x\).

2) Если \(y <0\), то 

\(x^2+y^2-1\le 0\)

\(x^2+y^2 \le 1\)

\(x^2+y^2 = 1\) - окружность с центром \((0; 0)\) и радиусом \(1\).

б) \(x(x^2-y)\le 0\)

1) Если \(x\ge 0\), то

\(x^2-y\le 0\)

\(-y \le - x^2\)  \(/\times (-1)\)

\(y \ge x^2\)

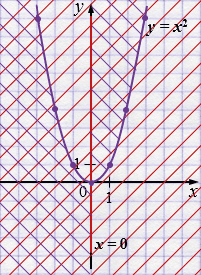
\(y = x^2\) - парабола, ветви вверх.

2) Если \(x < 0\), то

\(x^2-y\ge 0\)

\(-y\ge -x^2\) \(/\times (-1)\)

\( y\le x^2\)

\(x = 0\) - ось \(y\).

Пояснения:

Используем правило для произведения:

• \(ab\ge 0\) только тогда, когда \(a\ge 0 \text{ и } b\ge 0\) или \(a\le 0 \text{ и } b\le 0\).

• \(ab\le 0\) только тогда, когда \(a\ge 0 \text{ и } b\le 0\) или \(a\le 0 \text{ и } b\ge 0\).

а) Здесь \(a=y\), \(b=x^2+y^2-1\). Второй множитель обращается в ноль на окружности \(x^2+y^2=1\). Он положителен вне окружности и отрицателен внутри. Поэтому:

— при \(y\ge 0\) нужно брать те точки, где \(x^2+y^2-1\ge 0\), то есть верхнюю полуплоскость вне единичной окружности;

— при \(y < 0\) нужно брать те точки, где \(x^2+y^2-1\le 0\), то есть нижнюю полуплоскость внутри единичной окружности.

Получаем множество решений:

вне (или на) окружности \(x^2+y^2=1\) при \(y\ge 0\),

и внутри (или на) окружности \(x^2+y^2=1\) при \(y\le 0\),

а также все точки прямой \(y=0\) и всей окружности \(x^2+y^2=1\).

б) Здесь \(a=x\), \(b=x^2-y\). Второй множитель равен нулю на параболе \(y=x^2\). Выражение \(x^2-y\le 0\) равносильно \(y\ge x^2\), а \(x^2-y\ge 0\) равносильно \(y\le x^2\). Поэтому:

— при \(x\ge 0\) нужны точки, где \(y\ge x^2\) (правая половина плоскости над параболой);

— при \(x < 0\) нужны точки, где \(y\le x^2\) (левая половина плоскости под параболой).

Получаем множество решений:

при \(x\ge 0\) — точки на или выше параболы \(y=x^2\),

при \(x\le 0\) — точки на или ниже параболы \(y=x^2\),

а также все точки прямой \(x=0\) и всей параболы \(y=x^2\).

Построение границы: если неравенство нестрогое (\(\ge\) или \(\le\)), то линия, соответствующая графику уравнения, входит в решение (рисуем график сплошной линией).