Упражнение 406 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№406 учебника 2023-2026 (стр. 123):
Укажите три значения \(c\), при которых прямая \(y = c\) и окружность \(x^2 + y^2 = 9\):
а) пересекаются;
б) не имеют общих точек.
При каких значениях \(c\) прямая касается окружности?
№406 учебника 2014-2022 (стр. 113):
Докажите, что графиком уравнения \(x^2 + y^2 - 6(x - y) = 7\) является окружность.
Подсказка
№406 учебника 2023-2026 (стр. 123):
Вспомните:
- Что называют решением системы уравнений с двумя переменными.
- Метод подстановки при решении систем уравнений.
- Координаты точки на координатной плоскости.
- Уравнения с двумя переменными, их свойства.
- Степень с натуральным показателем.
- Линейную функцию, ее график.
- Уравнение окружности, ее график.
- Решение неравенств второй степени.
- Квадратичная функция, ее график.
- Неполные квадратные уравнения.
- Арифметический квадратный корень.
- Числовые промежутки.
№406 учебника 2014-2022 (стр. 113):
Вспомните:
- Уравнения с двумя переменными.
- Уравнение окружности.
- Квадрат суммы и квадрат разности двух выражений.
- Распределительное свойство умножения.
- Степень с натуральным показателем.
Ответ
№406 учебника 2023-2026 (стр. 123):
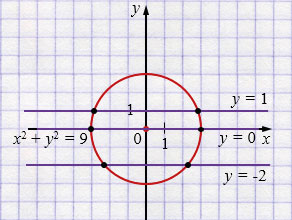
\(y = c\) и \(x^2 + y^2 = 9\)
\( \begin{cases} x^2 + y^2 = 9, \\ y = с \end{cases} \)
\( \begin{cases} x^2 + с^2 = 9, \\ y = с \end{cases} \)
\( \begin{cases} x^2 = 9 - с^2, \\ y = с \end{cases} \)
а) Пересекаются:
\(9 - c^2 > 0\)
\(y = 9-c^2 \) - парабола ветви которой направлены вниз.
\(9-c^2 = 0\)
\(c^2 =9\)
\(c = \pm\sqrt9\)
\(с = \pm3\)
\(c \in (-3; 3)\)
Прямая и окружность пересекаются при \(c = 0,\; c = 1,\; c = -2\).
б) Не имеют общих точек:
\(9 - c^2 < 0\)
\(y = 9-c^2 \) - парабола ветви которой направлены вниз.
\(9-c^2 = 0\)
\(c^2 =9\)
\(с = \pm3\)
\(c\in(-\infty; -3) \cup (3; +\infty)\)
Прямая и окружность не имеют общих точек при \(c = 4,\; c = -5,\; c = 7\).
Касание окружности:
\(9 - c^2 = 0\)
\(c^2 = 9\)
\(c = \pm3\)
Прямая касается окружности при \(c = 3\) и \(c = -3\).
Пояснения:
Используемые правила:
1. Окружность \(x^2 + y^2 = r^2\) имеет радиус \(r\) и центр в начале координат.
2. Прямая \(y = c\) — горизонтальная прямая (параллельна оси \(x\)).
3. Число общих точек определяется числом решений уравнения \( x^2 = 9 - с^2\), полученного после подстановки.
Подробное объяснение:
После подстановки \(y=c\) получаем уравнение \(x^2 = 9 - c^2\).
Если правая часть положительна, уравнение имеет два решения по \(x\), значит прямая пересекает окружность в двух точках.
Если правая часть отрицательна, решений нет, значит прямая и окружность не имеют общих точек.
Если правая часть равна нулю, уравнение имеет одно решение, значит прямая касается окружности.
№406 учебника 2014-2022 (стр. 113):
\(x^2 + y^2 - 6(x - y) = 7\)
\(x^2 + y^2 - 6x + 6y = 7\)
\( (x^2 - 6x + 9) - 9 + (y^2 + 6y + 9) - 9 = 7\)
\((x - 3)^2 + (y + 3)^2 - 18 = 7\)
\((x - 3)^2 + (y + 3)^2 = 7 + 18\)
\((x - 3)^2 + (y + 3)^2 = 25\)
\((x - 3)^2 + (y + 3)^2 = 5^2\) - окружность с центром в точке \((3; -3)\) и радиусом \(r=5\).
Пояснения:
Уравнение окружности имеет вид:
\((x - a)^2 + (y - b)^2 = r^2\).
Чтобы убедиться, что данное уравнение описывает окружность, нужно привести его к этому виду.
Для этого раскрываем скобки и, учитывая то, что выражение не изменится, если к нему прибавить и вычесть одно и то же число, выделяем квадраты двучленов:
\(a^2 + 2ab + b^2 = (a+b)^2\),
\(a^2 - 2ab + b^2 = (a-b)^2\).
Вернуться к содержанию учебника