Упражнение 463 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 137

а) \( \begin{cases} x \ge 2,\\ x \ge 1; \end{cases} \)

б) \( \begin{cases} x < -1,\\ y > 0; \end{cases} \)

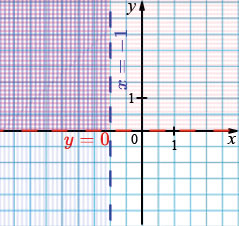
в) \( \begin{cases} x + 2 \ge 0,\\ y - 3 \le 0 \end{cases} \)

\( \begin{cases} x \ge -2,\\ y \le 3 \end{cases} \)

Пояснения:

1. Неравенства вида \(x \ge a\), \(x < a\) задают вертикальные полуплоскости.

2. Неравенства вида \(y \ge b\), \(y < b\) задают горизонтальные полуплоскости.

3. Решение системы — пересечение соответствующих полуплоскостей.