Упражнение 397 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 122
Вернуться к содержанию учебника
Вопрос
Решите графически систему уравнений
\(\begin{cases} x^2 + y^2 = 100,\\ y = \dfrac{1}{2}x^2 - 10. \end{cases}\)
Подсказка
Вспомните:
- Что называют решением системы уравнений с двумя переменными, графический способ решения систем уравнений с двумя переменными.
- Координаты точки на координатной плоскости.
- Уравнения с двумя переменными, их свойства.
- Уравнение окружности, ее график.
- Квадратичная функция, ее график.
- Степень с натуральным показателем.
- Вычитание рациональных чисел.
- Умножение обыкновенных дробей.
Ответ
\(\begin{cases} x^2 + y^2 = 100,\\ y = \dfrac{1}{2}x^2 - 10. \end{cases}\)
\(x^2 + y^2 = 100\) - окружность с центром в точке \((0; 0)\) и \(r = 10\).
\(y = \dfrac{1}{2}x^2 - 10\) - парабола, ветви которой направлены вверх.
| \(x\) | \(-6\) | \(-4\) | \(-2\) | \(0\) | \(2\) | \(4\) | \(6\) |
| \(y\) | \(8\) | \(-2\) | \(-8\) | \(-10\) | \(-8\) | \(-2\) | \(8\) |
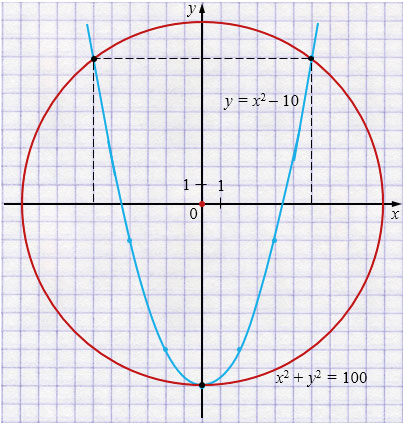
Ответ: \((0; -10)\), \((6; 8)\), \((-6; 8)\).
Пояснения:
Уравнение \(x^2 + y^2 = 100\) задаёт окружность радиуса \(10\) с центром в начале координат.
Уравнение \(y = \dfrac{1}{2}x^2 - 10\) задаёт параболу, ветви которой направлены вверх, вершина находится в точке \((0;-10)\). Строим параболу по точкам, составив таблицу.
При графическом построении видно, что парабола касается окружности в точке \((0;-10)\) и пересекает её ещё в двух симметричных точках \((6;8)\) и \((-6;8)\).
Вернуться к содержанию учебника